[物理]無次元化の方法と具体例

概要

力学などの物理現象のシミュレーションでは、無次元化を行う事が多い。これにより、物理の方程式中から、極端に大きい（小さい）パラメータが消え、計算精度の向上が見込まれる。

今回は、無次元化の方法と、具体例について調べた。

無次元化とは、方程式中に現れる変数を無次元量に置き換える事である。

一部の例外を除き、物理で使われるパラメータには単位が存在し、物理量は以下の７つの基本単位かそれらの積・商で表される

無次元化では、上記の単位及びそれらの積・商を利用し、（単位のある変数）=（単位のある定数）×（無次元変数）
の形に置き換える事で行う。その具体例を次の節で示す。

今回は、天体からの引力に引かれる物体を考える。（下図）

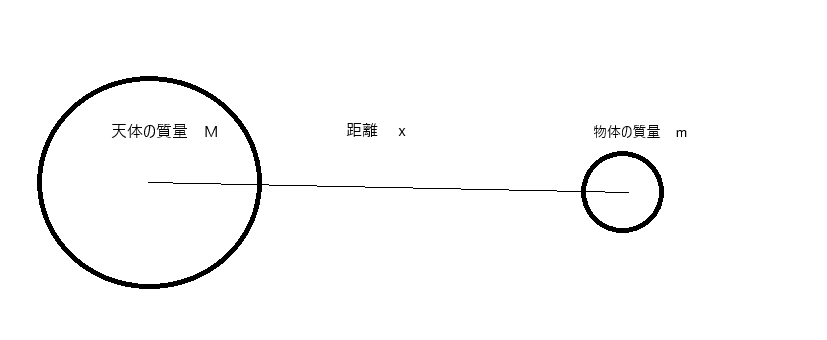
天体の質量は物体に比べて十分に大きく不動な物と近似できるとする。また、物体の初期位置をx ₀ とする。

この場合、物体の運動方程式は以下のようになる。

(2-1)

これをもとに無次元化を行っていく。

まず、式に含まれている、変数が持つ単位はx,tで、それぞれの単位は距離と時間であるのでこれらを定数である、質量・初期位置及び万有引力定数を用い無次元化する必要があると分かる。

ここで物体の初期位置を使い、xを単位のある量(x ₀ )と、単位を持たない量(x’)にわけると以下のようになる。

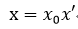
(2-2)

次に時間、ｔを無次元化していく。

そのために、定数のうち、時間の単位を含む物を探す必要がある。

万有引力定数Ｇの単位は、 N m　²　 kg ^-2=(Kg m s ^-2 )m ² kg ^-2 であるので、時間を含むとわかる

上で求めた単位をもとに定数を用いて、時間の単位を持つ量を作ると以下のようになる。

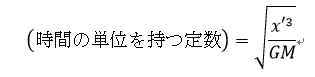
(2-3)

これを使い、時間tを以下のように置き換える。

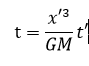
(2-4)

これら、x　,tを元の運動方程式に代入していく。時間微分が式2-5のようになることに注意しつつ、式を整理すると式(2-6)のようになる。

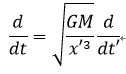
(2-5)

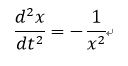
(2-6)

ここで上式と元の運動方程式を見比べると、各種定数（初期位置・質量及び万有引力定数）に依らない式を作ることが出来たことになる。

後はこれをもとに数値解析等を行うことになる。