My portfolio

Menu▼

  • Top
  • About
  • Portfolio
  • Diary
  • Privacy policy

    • [数値解析]エクセルVBAによるニュートン法の実装

    概要

    　非線形方程式の有効な解法の１つにNewton法というものがある。 今回は、関数f(x)=xe x に対し数値解析を行った。

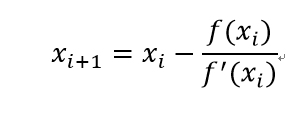    家事を粉づためのtodoリスト Newtonの反復公式
    反復計算により関数f(x)=0解を求める

    ニュートン法

    ある関数の解をα、それの近似値をx iと置くと関数f(x)のx=α近傍でのテイラー展開は以下のようになる。

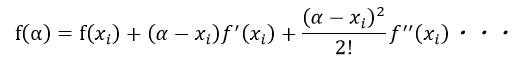
    テイラー展開の式

    (1-1)

    ここで、(α-x i )が十分に小さい時、式1-1の右辺の第３項以降は無視できる。 さらにf(α)=0を用いると、以下のようになる。

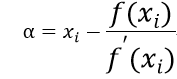    ニュートン法の式 (1-2)

    これにより、概要で示したNewtonの反復公式が得られる。

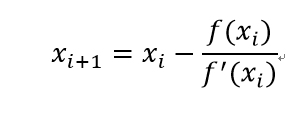
    ニュートン法の反復公式

    (1-3)

    収束条件

    Newtonの反復公式の右辺を次のように書く。

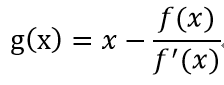
    ニュートン法公式の右辺

    （2-1）

    これを用いると、Newtonの反復公式が収束するための条件は、 |g ' (x)| < 1(2-2)とかける。

    g ' (x)を求めると、以下のようになる。
    ここで、f ' (α)≠0であれば、f(α)=0より式(2-2)を満たす。

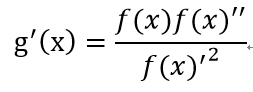
    ニュートン法微分

    (2-3)

    エクセルVBAによる実装

    概要でも書いた通り、関数f(x)=xe x -c(ｃは定数)に対し、Newton法で計算を行った。

    今回はxe x -1=0(c=1の時)について計算を行った。

    またxの初期値x 0 は10、計算完了の判定として、|x i e x i-1| < 0.0001を用いた。

    計算の結果は、x=0.567である（下のエクセル）。なおこの値はf(x)=xe x の逆関数であるランベルトのw関数f -1(x)=w(x)のw(1)の場合の値と同じである。

    コード Private Function targetFunc(X As Double) '(xe^x)-右辺　の計算を行う targetFunc = (X * Math.Exp(X)) - RightSide_ End Function Private Function differ(X As Double) differ = Math.Exp(X) + (X * Math.Exp(X)) End Function 'ニュートン法 Public Function doNewTonMethod() As Boolean Step_ = Step_ + 1 doNewTonMethod = False '収束していない場合はFalse Dim val As Double val = targetFunc(X_) If val < 0.0001 Then doNewTonMethod = True Exit Function End If X_ = X_ - (val / differ(X_)) End Function

    ダウンロード
    *事前に規約をお読みください

    ニュートン法のプログラムが入ったエクセルマクロファイルがダウンロードできます