[物理]ケプラーの法則の導出
概要
ケプラーの法則とはヨハネス・ケプラー（1571～1630）が発見した天体の運動についての法則である。
法則は下記のように３つあり、これらは運動方程式から導出できる。
- 運動方程式
- 第一法則
- 第二法則
- 第三法則
目次
運動方程式
ケプラーの法則の導出に当たって、運動方程式を記述していく。
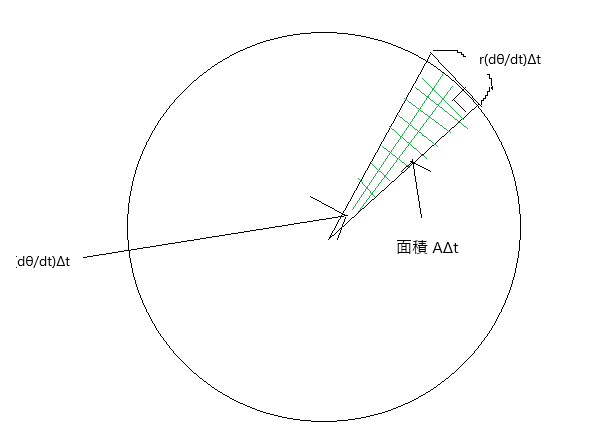
ここでは、主星を原点とした極座標で惑星の座標を表し、それを元にラグランジュ形式の運動方程式を立てる。(下図)
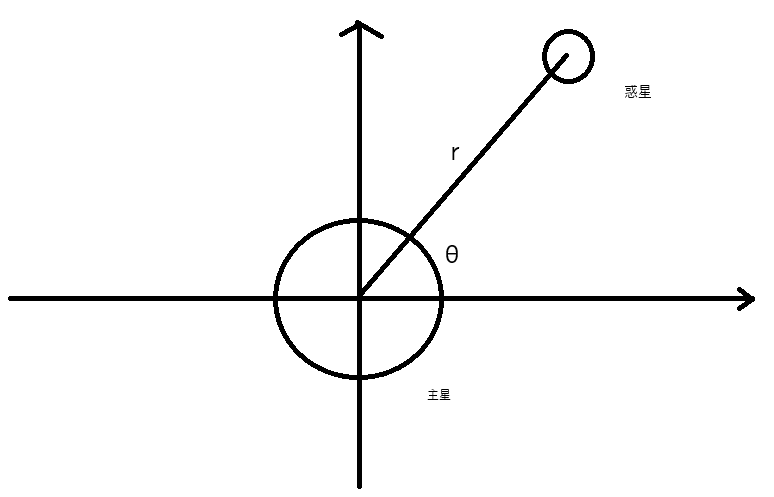
まず主星を原点とした惑星の位置を極座標で書くと以下の式のようになる。
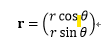・・・1-1
次に式1-1を時間微分し速度を求めると以下の式のようになる。
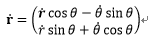・・・1-2
また惑星の位置エネルギーは式1-3のように書ける。
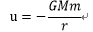・・・1-3
よってラグランジアンは次式で書ける。
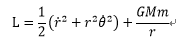・・・1-4
以下、これを元に運動方程式を作る。
まずθについては次のようになる。
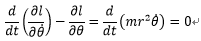・・・1-5
rについても同様に運動方程式を求めると次のようになる。
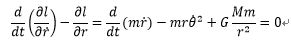・・・1-6
以降のセクションでは式1-5,1-6を元にケプラーの法則を導出していく。
第一法則
式1-5より、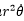
は時間によらず一定と分かる。
ここで下図より、この値は主星と惑星を結ぶ線が単位時間に掃く面積（面積速度）の半分と分かる。
これはケプラーの第一法則そのものである。
以降の説明のため、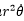 を面積速度Aを用いて以下のように書く。
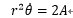・・・2-1
第二法則
式1-6に式2-1を代入し両辺をmで割ると次式のようになる。
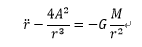・・・3-1
ここで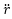
を消すために以下のような計算をする。
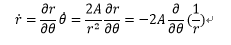・・・3-2
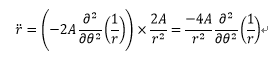・・・3-3
なお、上式の変形で式2-1を用いた。これで式3-1から 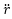を消す準備が出来た。
ここで、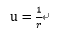
・・・3-4 と置き、3-3を3-1へ代入すると以下のようになる。
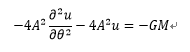・・・3-5
ここで上式の両辺を-4A 2 でわり、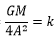
・・・3-6と置くと下式のようになる。
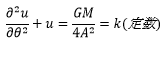・・・3-7
これは外力下における単振動の方程式と同じ形で、解は以下のようになる。
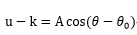・・・3-8
ここで、式3-4を用い、rを求めると次のようになる。
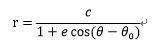・・・3-9
ここで、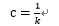
・・・3-10 及び 
・・・
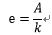3-11を用いた。
式3-9は曲方程式であり、0 < e < 1の時に楕円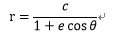 
・・・3-12 をθ 0
だけ回転させたものとなる。これによりケプラーの第二法則が導出できる事が分かる。
第三法則
第三法則は、第一法則と、第二法則を元に導出できる。
具体的には第二法則により求まった楕円の面積を面積速度で割ることにより導出できる。
まず式3-12を以下のように変形する。
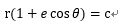・・・4-1
ここでx=rcosθを用いると次のようになる。
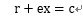・・・4-2
ここでx 2 +y 2 =r 2に注意し式4-2を２乗すると次のようになる。
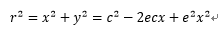・・・4-3
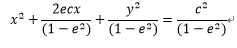・・・4-4
次に式4-4を変形し、(x-a) 2 +(y-b) 2=cの形に変形する。 今回は、b=0の形に変形できる。
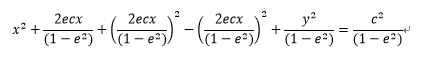・・・4-5
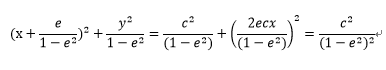・・・4-6
ここで式4-6を右辺が１になるように両辺を割ると次にようになる。
式4-7より楕円は
長半径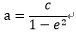 
・・・4-8
短半径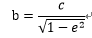 
・・・ 4-9
なので、面積は以下のように書ける。
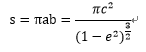・・・4-10
これで、公転周期と楕円の長半径の関係を求める準備が出来たので 式4-10を面積速度Aで割ったものを２乗する。そうすると次のようになる。
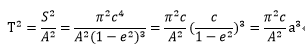・・・4-11
ここでさらに、式3-6,3-10を用いると、以下のようになる。
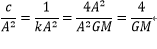・・・4-12
式4-12を式4-11に代入すると以下のようになる。
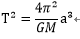・・・4-13
式4-12に置いて、同じ主星の元公転している惑星であればMは惑星間で共通点であるため、
T^２乗はa^3に比例すると分かる。
これにより第三法則が導出できる。