My portfolio

Menu▼

  • Top
  • About
  • Portfolio
  • Diary
  • Privacy policy

    • [数値解析]離散フーリエ変換（DFT）の実装と
    エイリアシングエラー

    概要

    フーリエ解析を用いることで、振動現象の解析や、ランダムに見える現象に周期性を見いだせる事がある。

    しかし連続量の観測であっても、得られるデータは離散的である。
    このため、離散データに対しフーリエ変換を行う必要がある。

    今回はその手段の１つである離散フーリエ変換（DFT）について調べた。

    連続関数のフーリエ変換

    離散フーリエ変換について述べる前に連続関数のフーリエ変換について説明する。

    ある周期２πの関数f(t)を考える。 この関数が、三角関数を用いて以下の形(式1-1)で書けると仮定する。

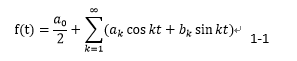
    次に、上式の両辺に三角関数を掛け、以下の計算をする。

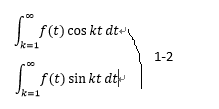
    ここで、三角関数の以下の性質（式1-3）を利用すると、係数a k ,b kが求まり、式1-2は1-4のように変形できる。

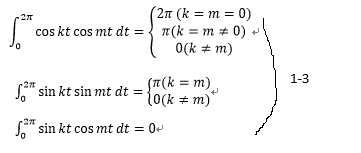
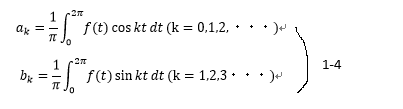
    離散フーリエ変換

    連続データのフーリエ変換を元に離散フーリエ変換（DFT）を行う方法を考える。

    まず前項で扱った関数を区間等間隔で分割する。
    分割した点に順番に番号j(j=0,1,2,・・・)を割り当てる(下図)。

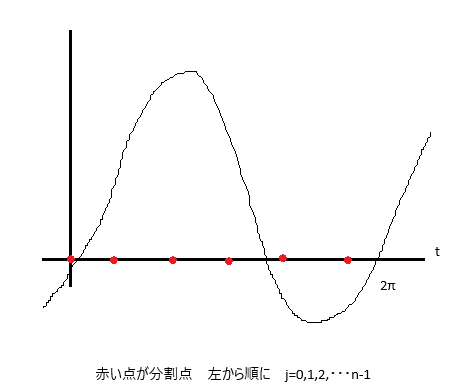
    この時、区間[0,2π]での分割データ数を2nとすると、tとｊの間には以下の関係がある。

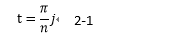
    これを、式1-1に代入すると、下式のようになる。

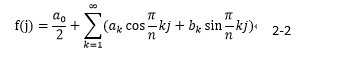
    ここで、上式を離散フーリエ級数で表した物が以下のようになると仮定する。
    （式2-2と異なり、kの範囲に上限がある事と、A nの項が追加されている事に注意。）

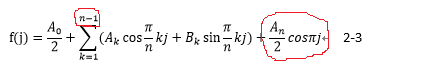
    ここで、連続関数と同様に係数を求めると、以下のようになる。

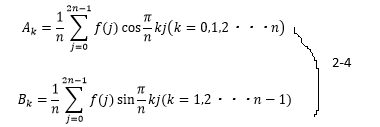
    ここでも、ｋの値に上限がある。また、A k とB k でkの範囲が異なる事にも注意が必要。

    エイリアシング

    式2-4の各係数を、式2-2の係数を使って表す。
    式2-3のk=K( > 0)の項と、式2-2のk=K,2nj ±Kの項を比較する為に、式2-2,2-3を以下のように変形する。

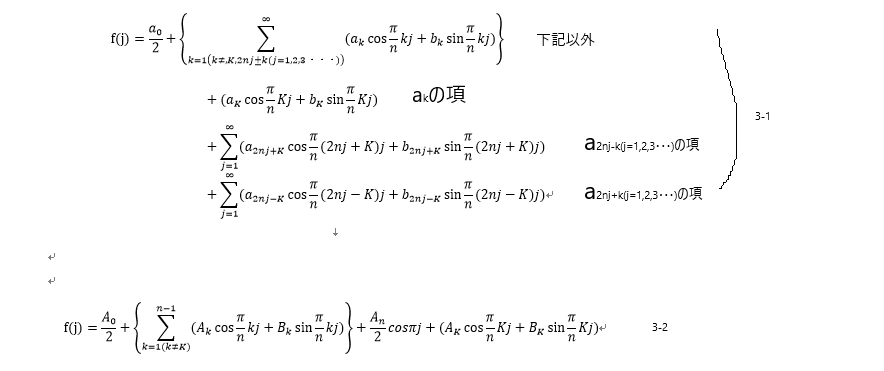
    ここで、 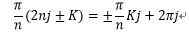に注意しつつ、上式を比較すると以下の関係が成立すると分かる。

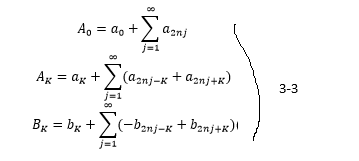
    ここで、次に式2-2においてk ' < nとなる成分(a k ' ,bk ')について考える。
    この時、2nj-k > =n > k ' ,2nj+k > n > k ' であるので、式3-3の 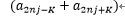に、a k ' ,b k 'が現れる事はない。
    逆にa k ,b kの項に現れる。

    次にk’ > nとなる成分、a k ',b k 'について考える。
    この時、式3-3の 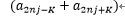内に2nj±k=k’となるkが存在する。
    逆に上式のa k ,b kには存在しない。

    また、同時にak’,bk’以外の成分（a k '',b k ''）も同時に存在する事になる。(下図)
    これは、２つの周波数成分(k’とk’’)を分離出来ないことを意味する。

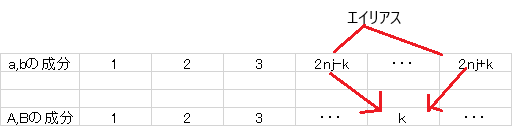
    このように、分割数2nの時、nより大きい周波数成分を分離出来ない事をエイリアシングという。

    また、上の例のように混同される周波数成分(k’とk’’)をエイリアスと言う。

    プログラム作成

    前項を元に、離散フーリエ変換を行うプログラムを作成した。 今回は変換する関数を以下のようにした。

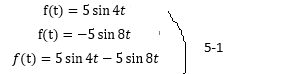
    今後の機能追加（入力関数の表示や線形代数の利用）の事を考え、今回は、式3-4を行列で表した式（式5-2）を用いた。

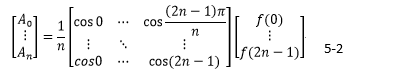
    Bについても同様。

    分割数を12（n=6）としてプログラムを実行した結果、確かにBk=bkである事が分かる。
    次に分割数を6(n=3)とすると、エイリアシングエラーが生じ、b 4 ,b 8 の両方の成分が係数B 2 として求まり、両者を分離できないと分かった。（今回の場合は j=1,k=2）

    コード

    DFTコード using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; using System.Windows.Forms; namespace DFT { internal class DFT_Cal { int n; double[,] matrix_C;//C:cos double[,] matrix_S;//S:sin double[] ket_IN;//入力ケットベクトル（関数） double[] ket_A;//出力ケットベクトル（係数A） double[] ket_B;//出力ケットベクトル（係数B） System.Windows.Forms.Label message; public DFT_Cal(int n, ref System.Windows.Forms.Label messagaBox) { //分割数をここで指定 message = messagaBox; this.n = n/2; matrix_C = new double[this.n+1,2*this.n];//行列を作成(0~n行,0~2n-1列) matrix_S =new double[this.n-1,2*this.n];//上記同様な行列を作成(1~n-1行,0~2n-1列) ket_IN = new double[2*this.n];//ケットベクトルを作成 ket_A = new double[2*this.n]; ket_B = new double[2*this.n]; for(int k = 0; k <=this.n; k++)//i行 { for(int j = 0; j <= (2*this.n)-1; j++)//j列 { matrix_C[k,j] = (double)(Math.Cos((Math.PI *k * j) /this.n))/this.n; } } for (int k = 1; k <= this.n - 1; k++) { for(int j = 0; j <= (2*this.n)-1; j++) { matrix_S[k-1,j]=(double)(Math.Sin((Math.PI * k * j) /this.n))/this.n; } } message.Text = "行列作成完了"; } public void SetFunction() { for (int j = 0; j <= (2 * this.n) - 1; j++) { double t = (Math.PI / this.n) * j; ket_IN[j] = 5 * Math.Sin(4 * t);//ここの関数を様々な物に変える } message.Text = "関数セット完了"; } public void CalcCoefficient() { for (int k = 0; k <= this.n; k++) { for (int j = 0; j <= (2 * this.n) - 1; j++) { ket_A[k] += matrix_C[k, j] * ket_IN[j]; } } for(int k = 1;k <= this.n-1; k++) { for(int j = 0; j <= (2 * this.n) - 1; j++) { ket_B[k - 1] += matrix_S[k-1,j]*ket_IN[j]; } } message.Text = "係数計算完了"; } public double getA(int index) { return ket_A[index]; } public double getB(int index) { return ket_B[index-1]; } } }