My portfolio

Menu▼

  • Top
  • About
  • Portfolio
  • Diary
  • Privacy policy

    • [プログラム]RSA暗号の数学的な説明と
    ExcelVBAによる実装

    概要

    　古来から人類は他者と情報のやり取りをする際、やり取りの内容が第三者に知られないように暗号を作成してきた。
    単純な替え字暗号や機械を使用したエニグマ暗号まで様々な工夫を凝らし、暗号が解読されないようにしてきた。

    　ところがこれらの暗号には欠点があり、暗号文の作成・復号に使う鍵を送信者と受信者で共有しておく必要が有ることである。
    この欠点により、鍵をどのようにして相手に安全に送るかという問題が出てくる。

    　RSA暗号では、第三者に公開する鍵(公開鍵)と受信者のみが持つ鍵(秘密鍵)の２つの鍵を作成する。公開鍵の内容から秘密鍵を推定する事は困難である。また、公開鍵による暗号の作成手順を逆にたどり、暗号文から平文に戻すことは不可能なようになっている。
    これにより公開鍵は第三者の目に触れても問題ないようになっているため、鍵の輸送問題を解決できる。（図）

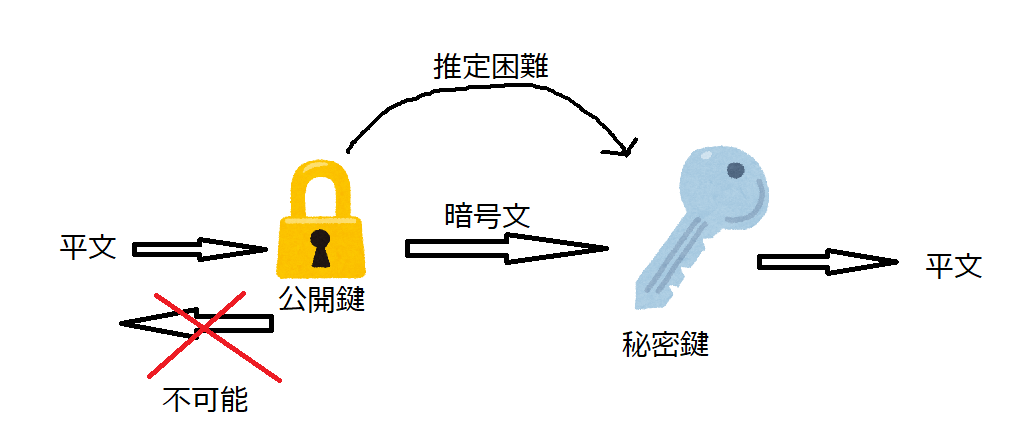
    　今回はRSA暗号の仕組みについて調べた。また暗号を作成するプログラムも作成したので報告する。

    RSA暗号の数学的な説明

    RSA暗号はある数を割った余りが持つ性質を利用している。

    割った余りを扱うための記号は≡ で、例えば は10を3で割った余りと7を3で割った余りが等しい事を表す。 また文脈上明らかな時は(mod 3)の部分を省略することもある。

    以下これを使ってRSA暗号の説明をする。

    まずある値の指数を取った後それを割ったものの性質には下式のようなものがある。

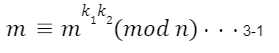    ただし、n,k 1,k 2は以下を満たす。 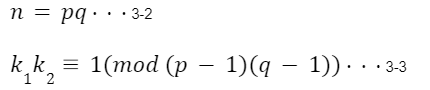また、k1は(p-1)(q-1)と互いに素である。
    証明

    n(=pq)は素数の積であるため、m≡m k1k 2 (mod p) かつ m≡m k 1 k 2 (mod q)を証明すればよい。 (m-mk 1 k 2がpの倍数かつqの倍数と考えれば分かりやすい。)

    以下、m≡m k1k 2 (mod p)証明する。

    mがpの倍数の時は明らかに成り立つ。以降はmはpの倍数でないとする。

    3-3より、k1k 2は(p-1)(q-1)で割ると１余るので、

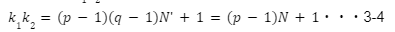
    ここでN=(q-1)N'と置いた。
    これを用いると、

    m k 1 k 2 =m (p-1)N+1=(m p-1) Nm

    m k 1k 2 ≡(m p-1) Nm (mod p)

    ここでフェルマーの小定理　補足を用いると、

    m p-1≡ 1(mod p)

    なので

    m≡m k1k 2 (mod p)

    が成り立つ。

    qについても同様。

    次にこれを暗号として使う方法を述べる。

    暗号としての用い方

    　概要に書いた通り、RSA暗号では秘密鍵と公開鍵の２つの鍵を用いている。
    上式（3-1〜3-3）を暗号として使うにあたって、公開鍵、秘密鍵として使うパラメータは以下のとおりである。

    　このようにすることで、悪意のあるものが公開鍵から秘密鍵を特定する際、nを素因数分解しp,qを特定する必要があることになる。
    一般的に大きな素数の積を素因数分解する事は困難であるため、通信の安全性が保たれる。

    　以下数字mを送信する際の手順を示す。
    また各手順で”m”に操作を加えた結果も併記する。 なお、m＜nとなるように適切なp、qを選ぶものとする。

    1. 受信側の操作その1
      1. 素数p、ｑを生成する。またn=pqとする。
      2. (p-1)(q-1)と互いに素な値k 1 を取ってくる。
      3. k 1 k 2 ≡1(mod (p-1)(q-1))となる、k 2を求める。
      4. n,k1を公開する。
    2. 送信側の操作
      1. 送りたい数字mをk 1乗し、nで割った余りを求める.。
        （操作結果）m→m k 1 mod n
      2. これを暗号文として受信側に送る。
    3. 受信側の操作その2
      1. 送られてきた暗号文をk 2 乗し、nで割った余りを求める。
        (操作結果)m k 1 mod n→m k 1k 2 mod n
      2. 式3-1よりこれが平文　
        (操作結果)m k 1 k 2mod n→m mod n=m

    エクセルvbaを用いた実装

    これまでの記述をもとにExcelVBAで、RSA暗号を送受信するプログラムの作成を行った。

    今回は、RAS暗号で暗号文そのものを送るのではなく、共通鍵方式で用いる鍵を輸送する事を想定し、数値を一つ送ることにする。

    作成する関数

    今回のプログラムにおいて必要な機能を考え、必要な関数を整理した。
    今回作成した主な関数は以下の通り。

    1. 指数を計算しそれを指定した値で割った余りを求める関数。
      暗号の生成、復号の処理に用いる。
    2. ランダムな素数を求める関数。
      すでに生成された素数と重複しないようにする。これでp,qの生成を行う。
    3. ある数と互いに素な値を返す関数。これをk 1とする。
      素であるかの判定にはユークリッドの互除法 （補足） を用いる。
    4. k 1k 2≡ 1(mod (p-1)(q-1))となる、k 2 を求める関数。
      なおk 2 は必ず１つ見つかる。補足
      ループ文を用い探すが、上記の理由により、ループの終了判定にループ回数は不要。

    また、プログラム内のクラスの構成は以下の通り。

    1. 鍵を生成するクラス
    2. 生成した鍵をもとに暗号化＆復号するクラス。
      使用する鍵が異なるだけで、暗号化・復号ともに同じプログラムを使用できる。

    　上記の条件でプログラムを作成した結果、確かに暗号化・復号ができていることが確かめられた。

    　今回は生成した素数が小さいため解読は可能であるが、それでも手計算で素数を特定する事は非常に手間のかかる作業であることが分かった。
    例えば下の図の例では、素数の積は7387で、これをもとに7387=83×89を割り出す必要がある

    RSA暗号の実行結果

    　プログラムを作成している最中は、公開鍵で暗号化し、秘密鍵で復号する事を想定していたが、このプログラムをそのまま、秘密鍵で暗号化し、公開鍵で復号するプログラムとしても運用可能であることが分かった。（下記プログラム）

    暗号化＆復号プログラム Sub EncodeByPublicKkey() '公開鍵で暗号化し、秘密鍵で復号 Dim key As key Dim encoder As Corder Dim decoder As Corder Set key = New key '鍵を生成 Set encoder = New Corder Set decoder = New Corder '---公開鍵で暗号化--- encoder.k = key.k1 encoder.n = key.n encoder.Conversion (Range("A2")) '---秘密鍵で復号--- decoder.k = key.k2 decoder.n = key.n decoder.Conversion (encoder.conv) '----セルに書き込む----- Call writeCell(key.k1, key.k2, key.n, encoder.original, encoder.conv, decoder.conv) End Sub Sub EncodeByPrivateKkey() '秘密鍵で暗号化し、公開鍵で復号 Dim key As key Dim encoder As Corder Dim decoder As Corder Set key = New key '鍵を生成 Set encoder = New Corder Set decoder = New Corder encoder.k = key.k2 encoder.n = key.n encoder.Conversion (Range("A2")) decoder.k = key.k1 decoder.n = key.n decoder.Conversion (encoder.conv) '----セルに書き込む----- Call writeCell(key.k1, key.k2, key.n, encoder.original, encoder.conv, decoder.conv) End Sub

    補足

    鍵k2の生成とフェルマーの小定理

    鍵k2の生成およびフェルマーの小定理において重要な定理を示す。

    a,pを互いに素とする。この時

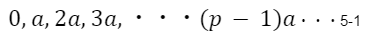
    をpで割った余りはすべて異なる。

    証明

    5-1をpで割った余りが同じになる物があったとする。この時以下の式が成り立つ。

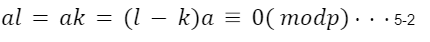
    ここで、aとpは互いに素、さらに0＜l-k＜p-1なので(l-k)aはpの倍数にならず、式5-2では矛盾が生じている。

    以上より最初の仮定は誤りであり、5-1をpで割った余りは、全て異なる。

    ここである数をpで割った余りは0〜(p-1)であるので、5-1をpで割った余りが1となる物が5-1の中に必ず1つあることになる。（k 1 k 2を求める際これを利用した）

    ここで5-1のうち、0以外の物をpで割った余りは1〜p-1であり、しかも重複しないので以下の式がなりたつ。

    ここで、pが素数の時、pと(p-1)!は互いに素なので、

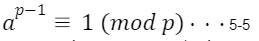
    となる。（フェルマーの小定理）

    なお、5-3から5-4の変形と5-4から5-5の変形でそれぞれ以下の事柄を使った。

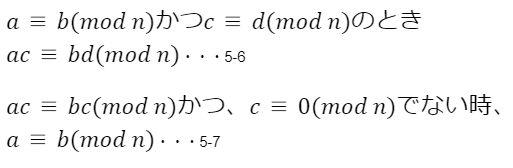
    ユークリッド互除法

    鍵k1を生成するには、２つの数字が互いに素であることを確認する必要がある。 今回はユークリッド互除法という方法を用い、最大公約数が１であることを確かめた。

    ユークリッド互除法とは以下の事実を利用して公約数を求める方法である。

    A=Bn+R・・・5-8とかけるとき、AとBの最大公約数はBとRの最大公約数と等しい。 ここでnはA/Bの商、RはAをBで割った余りである。

    今回作成したプログラムでは、ループ文中で
    A→B
    B→R
    と置き換えつつ、AmodB=0となるまで計算している。この時のBが求める最大公約数である。　

    ユークリッド互除法のプログラム Private Function CommondiVisor(ByVal A As Integer, ByVal B As Integer) As Integer 'ユークリッド互除法により最大公約数を求める Dim i As Integer If A < B Then i = B B = A A = i End If Do While A Mod B <> 0 'A→B 'B→R 'と置き換えつつA mod B=0まで繰り返す i = A Mod B A = B B = i Loop CommondiVisor = B End Function
    証明

    NをAとBの最大公約数とし、

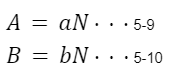
    と置く。

    上式5-9,5-10を5-8に代入すると以下のようになる。

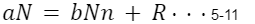
    よってRはNの倍数。
    ここで

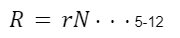
    と置く。

    次に rとbが互いに素でないと仮定する。
    この2つの約数をk(>1)とし

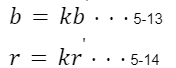
    を5-8に代入すると以下のようになる。

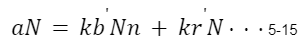
    ここでN＞0より、上式の両辺をNで割ると、

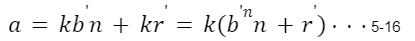
    上式よりaはkの倍数であるので、

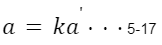
    と置ける。
    5-13と5-17を5-9,5-10に代入すると、

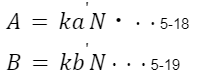
    となる。ここで、k>1であるので5-18,5-19の最大公約数N'は

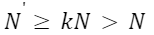
    とわかる。
    これはA,Bの最大公約数がNであることと矛盾するため仮定は誤りで、r,bは互いに素とわかる。

    よって5-10,5-12よりBとRの最大公約数はNであり、AとBの最大公約数と一致する。

    ダウンロード
    *事前に規約をお読みください

    注:あくまで勉強用のデモです、生成する素数が小さいためその気になれば手計算で解読可能です。