[C#]プログラムによる生物の遺伝シミュレーション
遺伝シミュレーション概要
生物の遺伝をモデルにし、ある個体(データ)の集団が持つ因子の存在割合が世代を経る毎にどのような変化をするか、C#を用いてシミュレーションを行った。 これにより、因子の存在割合は徐々に変化するのではなく、ある世代を境に急激に変化することが分かった。 これが生物の進化のモデルとしてどの位正しいかは不明であるが、面白い結果を得ることが出来た。
今回作成した因子の存在割合シミュレータ
- 因子の受け渡しモデル
- 各世代での因子の存在割合
- 解析結果
- 補足
- ダウンロード
- コード(C#)
目次
因子の受け渡しモデル
ある世代において、着目している種類の生物が持つ因子の種類をA,Bと置いた。各個体は通常の遺伝と同様に因子を二つ持ち、異なる種類の因子を持つ場合は優性遺伝の方が発現するものとする(下図)。加えて、発現した形質によって個体の生存率(子孫を残す前に死亡する確率)が異なる物とした。
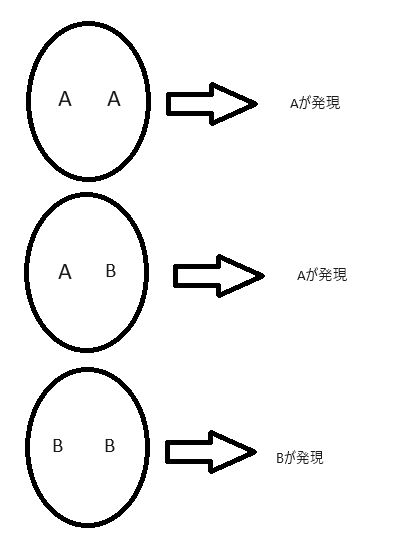
実際には血液型のように3種類以上の因子が存在する事もあるが今回は2種類の場合で考える。
また、因子A,B以外の因子によって生じた個体の形質によって個体の生存率は変化しないものとした。加えて、A,Bどちらの形質であっても、子孫を残すことが出来た場合、生まれてくる子孫の数は同じとする。例えば、形質Aより形質Bの方が卵を多く産む等の違いは存在しないものとする。
また生存率の変化は、個体が置かれている環境(気候、病原菌等)において子孫を残すのにどの程度有利かを表すパラメータであるが、今回のモデルでは、種の存在を脅かす(絶滅する)程生存に不利な状況は起きず、個体は十分な数が常に存在する物とする。
世代間での因子の引き継ぎ方法のモデルは、前の世代の個体が持つ因子をランダムで2つ(重複あり)で引き継ぐ物とした。このモデルでは、例えば個体の雄雌を考慮しない交配、近親交配、同一個体が持つ因子を2つとも引き継ぐ等の状況が含まれている。そのため親子間や親から孫のように数世代間での因子の受け渡しのモデルとしては不適切な部分がある、しかし何世代か先への引き継ぎのモデルと考えれば、良いモデルと考える。(以下数世代ずつを代表して親世代、子世代、またはi世代、i+1世代と言う)
例えば人間においても、自分の祖先を確認出来るのは通常は数世代前までである。言い換えれば、自分が持つ因子が数世代以上前の個体のどれに由来するか把握できる状況はほぼない。この事から、ある個体が持つ因子は、前の世代が持つ因子からランダムに2つ選んだものと近似して問題ないと考える。
各世代での因子の存在割合
まずある世代(親世代)の因子のうち次世代(子世代)に引き継がれるものの存在数をn A n B 、両者の合計をnとする。前述の通り次の世代の個体は前の世代の個体の因子をランダムで受け継ぐので、子世代の個体が持つ因子の組み合わせ別の分布は以下のようになる。(考え方は付録参照)
| 因子の組み合わせ | 存在割合 |
|---|---|
| AA | (P A) 2 |
| AB | 2P AP B |
| BB | (P B) 2 |
ただしここで、P k (k=A,B)は各因子の存在割合でそれぞれ以下のようになる。
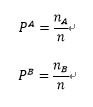
次に生存した子世代の個体の因子のみがさらに次の世代(孫世代)に引き継がれると考え子世代のn, n A ,n B及び、因子の存在割合(P k (k=a,b))を用い孫世代の状況を考える。 まず子世代の因子のうち、孫世代に受け継がれるものの個数(gene)を求める。これは各形質の個体の存在割合と生存率の積の合計であるを2倍したものである(下式)。
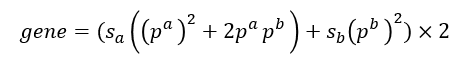
次に因子毎の引き継がれる割合を求めると次のようになる。
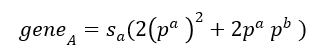
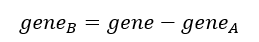
以上より孫世代での因子の存在割合P k (k=A,B)は次のようになる
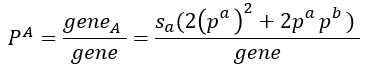
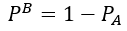
同様な考えを以降の世代にも適用しi+1世代目の因子の存在割合を求めると次のようになる、これをC#で解析した。
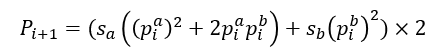
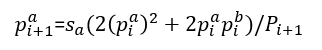
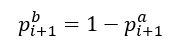
解析結果
今回の解析では、各因子に以下の初期条件を与え解析を行った。
| 因子A | 因子B | ||||
|---|---|---|---|---|---|
| 存在割合 | 生存率 | 存在割合 | 生存率 | 説明 | |
| 条件① | 9.99×10 -5 | 0.1 | 0.9999 | 0.09 | 優性遺伝による形質の方が生存に有利 |
| 条件② | 0.9999 | 0.09 | 9.99×10 -5 | 0.1 | 劣性遺伝による形質の方が生存に有利 |
*表示する桁の都合上、存在割合の合計は1にならない。
条件①について
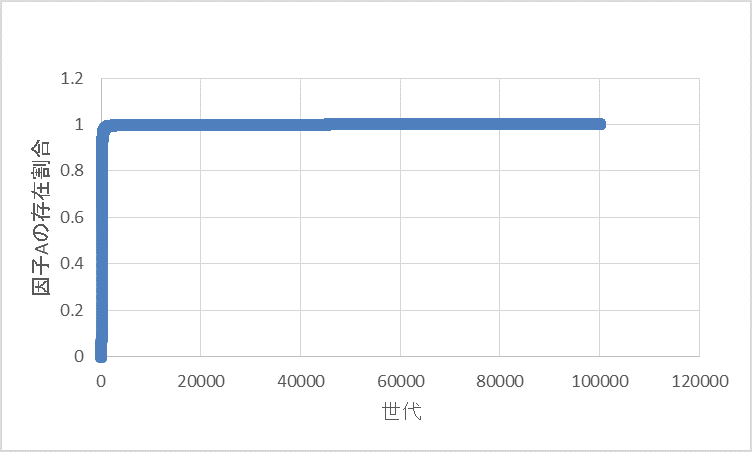
この条件は、形質Aの個体は初めはほぼ存在しないが、生存に有利な状況を想定している。
下のグラフが示すように、最初の数千世代で急激に因子Aの存在割合が増加し99%以上に到達する、その後はほぼ増加しない事が分かる。
条件②について
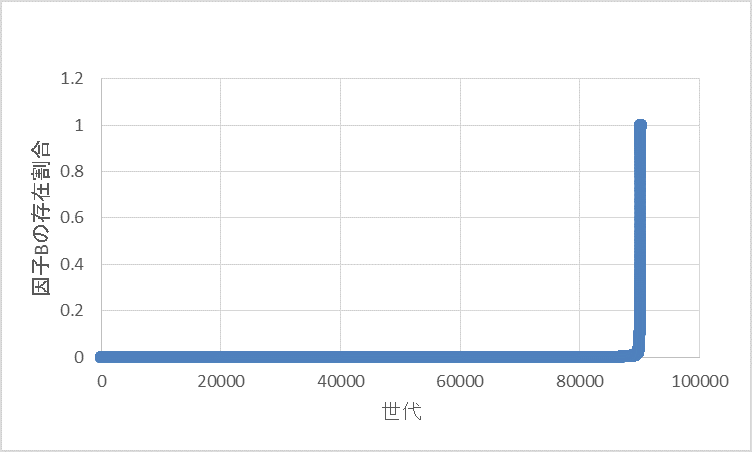
この条件は、形質Bの個体は初めはほぼ存在しないが、生存に有利な状況を想定している。
先ほどの条件とは対照的に、最初の方の世代ではほぼ存在割合が増加せず、9万世代付近から急激に因子Bの存在割合が増加することが分かる。
両方について
今回のシミュレーションの結果、因子の存在割合は徐々に増えるのではなくある世代で急激に増加し、その前後ではほとんど変化しないと分かった。 優性遺伝と劣勢遺伝で因子の存在割合が変化するタイミングが異なるが、これにより環境の変化に対する反応のしかたが異なり、優性遺伝の因子は短期的な環境の変化が起こればすぐに増加するのに対し、劣性遺伝では長期的な環境の変化が生じた時増加すると分かる。
補足 因子の組み合わせ別の存在割合
下の図のように子世代の因子の受け取り部分、(図の1,2の部分)に親世代からの因子を選び格納する状況を考える。 下図の場合は親の因子A,Bをそれぞれ子の因子の受け取り部分の1,2に格納している。
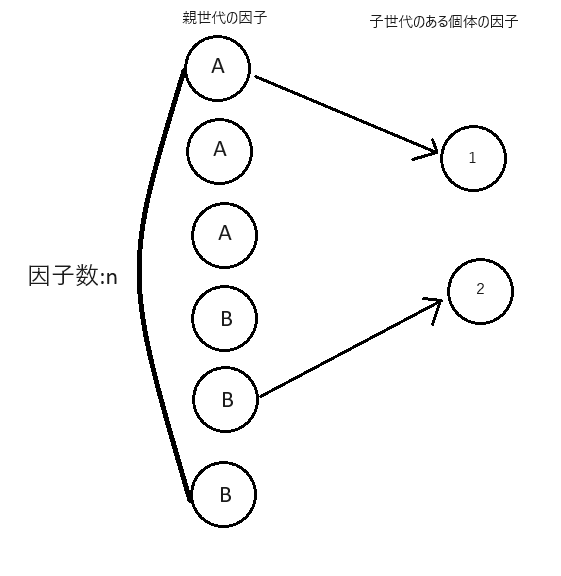
因子の組み合わせがA,Aとなる場合の数を考える。 因子Aの個数をn Aとすると、1に格納する因子の場合の数は
n A通りで1の格納する場合の数ぞれぞれに対し2に格納する因子の場合の数もn A通りある。以上よりこの組み合わせになる場合の数はn A 2通りになる。因子の組み合わせがBBの時も同様の考え方で、n B 2通りある。
因子の組み合わせがABとなる場合の数を考える。
まず1に因子A、2に因子Bを格納する場合の数はn An B通り。1に因子B、2に因子Aの場合も同様にn An B通り。
以上を合計して、2n An B通り。
これらの場合の数を 因子の受け取り方の場合の数であるn 2で割ると次の世代に受け継がれる各種因子の存在割合が求まる。