エクセルVBAによる微分方程式の数値解析 -ロケット方程式を題材に-
数値解析の概要
せっかくプログラムを習ったので、ゲーム以外にも応用しようと考えた。 題材を探していたところ、学生時代に使っていた物理の教科書が目に入った、そこで物理の式をプログラムで解いてみようと考えた。 今回のテーマは「ロケット方程式を立て、それをオイラー法と改良オイラー法を用い数値解析をする」とした。 卒業後全く物理をしていないので、リハビリとして今後も時々やると思います。 この記事のPDF版はコチラ
- ロケット方程式の導出
- 無次元化
- VBAを用いた数値解析
- あとがき
- VBA ダウンロード
目次
ロケット方程式の導出
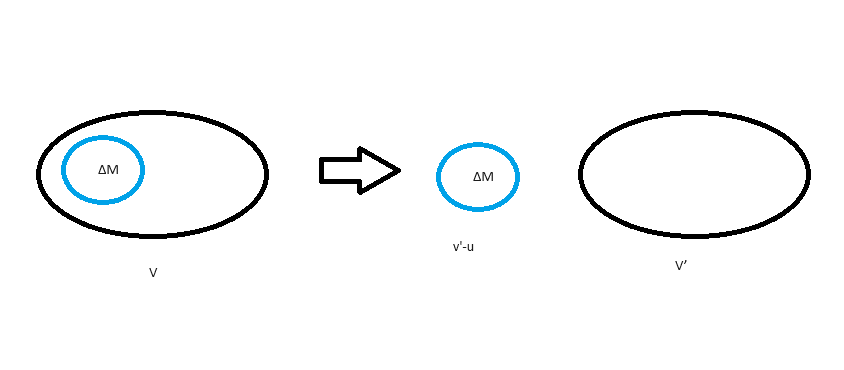
図のようにロケットから燃料をロケットに対する相対速度uで射出しながら加速する状況を考える。また射出した燃料の質量をΔmとする。
この時、燃料の射出前後でロケットと、燃料の運動量の合計は保存されるので、①式が成立する。
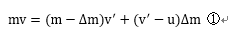
これをさらに変形すると、②式になる。
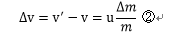
②式を用い微分方程式を立てる。(射出した燃料の質量)=-(ロケットの質量減少量)に注意すると、Δm=-dmが成り立つので、ロケット方程式は下のようになる。
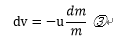
これを、数値解析し、その結果を微分方程式を解いた結果と比較する。
以下、この方程式を解く。まず③式の両辺を積分する。
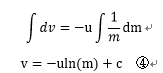
m=m 0 （初期質量）の時、v=0(停止)とすると、④式のcは以下のようになる。
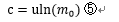
⑤を用いると④は以下のように書ける。
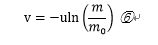
無次元化
③,⑥式をそのまま数値解析し比較しても良いがさらに変形する。まず、消費した燃料と、初期積載燃料の質量比を用いて速度を求めることが出来るようにする。
ある時の質量mは、消費した燃料の質量m ' (0≤m ' ≤(m 0 -m f ))と初期質量m 0及びロケット本体の質量m f
を用いて以下のように書ける。
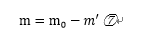
⑦を⑥に代入すると。次のようになる
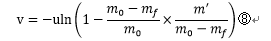
ここでmo -mf は初期積載燃料なので質量比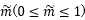 
を用いて書くと⑧は次のようになる。
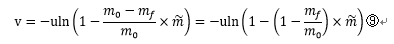
次に、速度をuとの比率で書く。以下の式⑩を⑨に代入すると、⑪になる
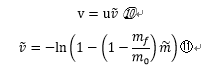
これにより、ロケットの全質量(m 0 )とロケット本体の質量(m f )の比率に依存し、燃料の噴出速度・消費した燃料の質量そのものに依存しない式ができた。
言い換えればm f/m 0 以外のロケットのスペックに依存しない式ができたことになる。
こうする事で、数値解析の結果を様々なスペックのロケットに対し使いまわすことが出来る。
最後に③式も、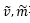
を用いた式に変形する。
⑦より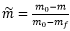 
なので
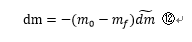
さらに⑩より、
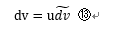
⑫、⑬を③に代入すると、⑭式ができる。
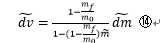
⑭の数値解析の結果と、⑪の計算結果を比較する。
VBAを用いた数値解析
今回は⑭式を、オイラー法と改良オイラー法を用い解析する。
オイラー法、改良オイラー法による数値解析の式はそれぞれ、⑮、⑯となる。
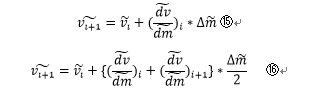
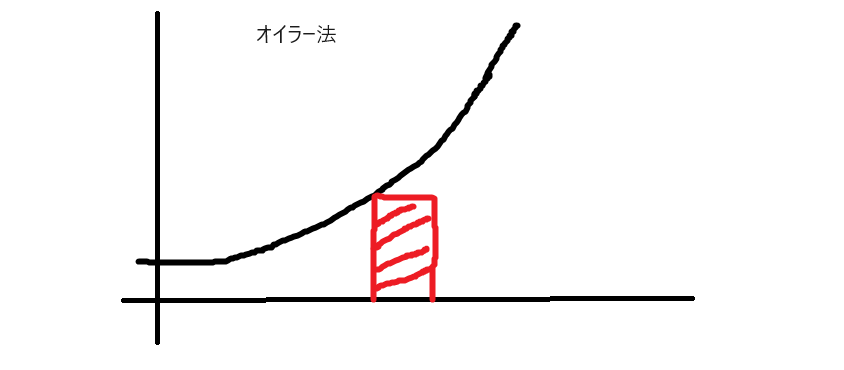
上式の図形的な意味は、
間の面積をそれぞれ長方形、台形で近似して求めることに相当する。
⑯において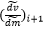 
は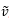 
を含まないので今回は楽に計算ができる。
通常は 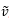を含むので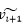
̃の値を、オイラー法等で予測したのち、⑯を使うことになる。
また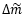 
は刻み幅で、今回の解析では0.01（燃料を初期積載量の1%消費に相当）としている。
実際には刻み幅で解析の精度が大きく変化するため、刻み幅を変化させ誤差を検証する必要がある。
今回は、ロケットの全質量のうち8割が燃料として解析した。
解析した結果、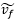 
=1.6程度になった。この結果を JAXAによるもの と比較すると、
- u=3430 (m/s)
- v f =5520(m/s)
であるので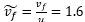 
となる。
これにより、誤差はオイラー法では約1%,改良オイラー法では約0.008%と分かった。
資料が残っていないので不確かだが 、学生時代別の式で同様な解析を行ったがもっと誤差が大きくオイラー法で数１０%、改良オイラー法で数％程度あったと記憶している。
今回の場合0.2≤⑭式≤0.25
で小さい値である事が要因であると考えた。
加えて前述のとおり、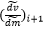 は 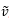を含まない為、 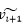を予測する必要が無く、 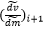を正確に計算できることも要因と考える。
また、図形的な意味を考えると、オイラー法は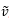 を過小評価、改良オイラー法では逆に過大評価気味と予測していたがその通りであった。
あとがき
管理人が、ロケットの最終速度は、全重量に対する燃料の割合で決まる事を知ったのは小学5,6年生の時と記憶している。空想科学読本２巻 の宇宙戦争をテーマにした記事に書いてあった。
当時は自力でこれを導き出すことは出来なかったが、可能になった。
また、単位を考慮すると、ロケット本体および燃料の質量のみではロケットの最終到達速度を記述することはできず、何らかの速度のパラメータが必要で下式の形かその変形であると予測することもできるようになった。
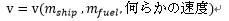
実家の本棚にまだ本が置いてあるので、また読み返そうと思った。 小学生の頃とは異なった読み方ができると思う。